- The variety of 2D networks, their structural topology, characteristics, classification, and nomenclature.
- The impact of the networks on the electronic properties and topological signatures.
- Tight-binding approach to band structure representation of 2D nets, including its extension to 2nd-neighbour interaction, spin–orbit coupling, and calculation of electronic topological properties using Chern numbers, Z2 invariants and nanoribbon approach.
- Realization of 2D nets in 2D polymers, the importance of building blocks, π-conjugation, and molecular connectivity.
- Building blocks design towards topological 2D polymers with signatures of corresponding 2D nets.
拓扑二维聚合物
马克西米利安·A·施普林格 Tsai-Jung Liu， Agnieszka Kuc and Thomas Heine *
摘要
有200多个具有不同拓扑的二维（2D）网络。2D网络的结构拓扑定义了其电子结构。包括电子拓扑特性，它产生了狄拉克锥，拓扑平坦带和拓扑绝缘体。在本教程审查中，我们展示了如何通过紧密绑定方法来计算2D网络的电子特性，以及当包含第二邻域相互作用和自旋轨道耦合时这些特性如何改变。我们解释了如何通过计算Chern数Z 2来确定所得的电子特征是否具有拓扑特征。不变性，并通过纳米带方法。本教程提供了一些建议，如何在由分子框架制成的显式原子化学2D系统中，特别是在2D聚合物中实现这种拓扑特性，在该2D聚合物中，给定2D网络的边缘和顶点被适当选择的分子构件取代并缝合在一起这样就保留了长距离π共轭。
学习重点
（1）各种2D网络，其结构拓扑，特征，分类和术语。
（2）网络对电子特性和拓扑签名的影响。
（3）二维网络的能带结构表示的紧束缚方法，包括其扩展到第二邻域相互作用，自旋轨道耦合，以及使用Chern数，Z 2不变量和纳米带方法计算电子拓扑性质。
（4）2D聚合物中2D网络的实现，构件的重要性，π共轭和分子连通性。
（5）具有相应2D网络特征的拓扑2D聚合物的构建模块设计。
1 引言
具有全新功能的材料的创建是化学的核心目标，在各个学科中都采用了实现功能的不同方法。例如，在有机和金属有机化学中，这些是官能团。它们与分子结构和其他特征（如芳香性）相互作用，是分子间相互作用的主要决定因素，因此，它们是控制反应性，选择性和催化性能的主要因素。在无机化学和固态物理学中，功能性是由材料的元素组成和网络中材料原子的排列共同赋予的。这对于具有多型体的材料是明显的，该多型体可以显示出非常不同的特性和功能。引人注目的例子包括绝缘钻石与导电石墨；灰色，易碎的α与金属的，易延展的β锡；或单层MoS 2的三种多型：半导体2 H，金属1 T和拓扑1 T ‘。这些多型体的不同特性和功能是由于网络连接性（配位）对电子系统的影响而产生的，在电子系统中，前沿电子决定了材料的特性。除了电子特性外，还有其他网络施加的特性，例如裂纹扩展，润滑或机械特性。1个
具有足够结晶度的骨架材料，特别是共价-有机骨架（COF）2–4和共轭二维（2D）聚合物5–7提供了结合分子和网络施加的功能的功能。2D COF和2D聚合物这两个术语都来自不同的社区，并且以非直观的方式使用。2D COF通常是指分层的材料，迄今为止通常缺乏长程的结晶顺序。另一方面，二维聚合物需要长距离顺序。8然而，迄今为止，关于框架材料的大多数报告都侧重于分子功能，而网络功能的潜力仍有待开发。虽然网络提供了机械稳定性和孔隙率，但对大多数框架材料的电子结构影响很小。对于准2D系统，这甚至是正确的，我们将在本文中重点介绍。
在最近的一些出版物中已经指出了网络拓扑结构对电子特性的潜在高影响，它们都集中在2D系统上。具有共轭电子系统5,9-11的 2D聚合物通常是半导体，它们可以具有高的载流子迁移率。网络拓扑可以施加有趣的电子结构，包括狄拉克点或平坦带。12-16然而，尽管已经报道了一些具有kagome（kgm）和蜂窝（hcb）晶格的二维聚合物，但迄今为止，尚未在实验中证明非平凡的电子拓扑结构。
障碍之一是结晶度，这是表现晶格依赖性电子特性所必需的。2D聚合物通常具有较小的晶体尺寸和较高的缺陷密度。但是，用于2D聚合物和2D COF的新合成方法可以使薄片尺寸达到几微米，并且缺陷密度低。17,18
即使可以使用高度结晶的骨架，也需要移动费米能级，使其与拓扑特征的位置（例如，平坦带或狄拉克点）相匹配。这可以在某种程度上通过外部手段来实现，例如通过电极或离子液体进行门控，但是可以通过单体的官能化更好地控制。12
本教程审查的目的是提供科学背景和理论工具箱，用于合理设计具有网络附加属性（包括拓扑属性）的2D聚合框架。为此，在第二部分中，我们将简要介绍各种合适的2D网络及其结构特征。在3 次部分，将介绍一个紧密结合（TB）的办法，来预测电子能带结构的网络强加的特征（用ESI给予技术教程一起†）。该TB模型是解决网络与电子结构之间关系的主要工具，并且还可以表征拓扑状态。在第4节中，我们将讨论如何通过改变晶格点之间的相互作用强度以及通过改变构件的化学势来在网络上操纵电子结构。在5 个部分中，我们将提供地图构建适合于形成各种2D网络块的，并已在文献中报道迄今2D聚合物的简短摘要，既计算和实验。最后，我们将在第6节中提供对拓扑2D聚合物新兴领域的未来的个人看法。
2 2D网络及其结构表征
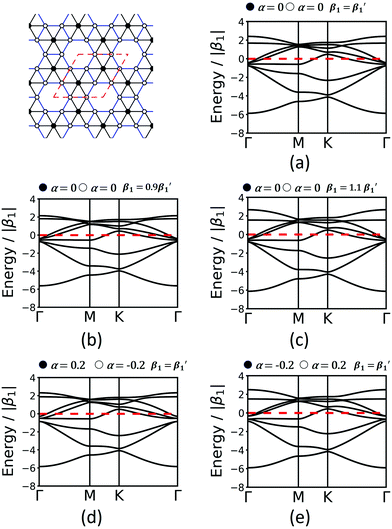
2D框架材料的拓扑可以通过镶嵌来描述。这些是多边形在平面上的周期性排列，没有重叠或间隙。顶点是两个以上的多边形相交的点。可以根据切片中使用的顶点和多边形的数量和种类对可能的镶嵌进行分类。19既可以仅通过使用规则多边形来构造平面网络，也可以使用不规则多边形。正多边形是等角的和等边的。为了用于网状化学，建立了网状化学结构资源（RCSR）。20它包含200个2D网络，每个网络都标有字母代码，将在此处使用。有四组仅使用规则多边形的网。第一组称为规则网（也称为柏拉图网，请参见ESI †中的表S1 ），仅包含一种类型的顶点和一种类型的规则多边形：六边形网（hxl，三角形），方形网（sql，正方形），和蜂窝网（HCB，六边形），参见图1。由于它们仅包含一种类型的顶点和一种类型的多边形（面），因此它们都是面和顶点可传递的。网络通常由其顶点的Schläfli符号来描述，该符号指定在该点相交的多边形的数量和顺序。例如，在hcb网（图1a）的每个顶点处，三个六边形的角相交，因此，网由符号6 3描述。半规则网由一种顶点类型和多于一种类型的面组成。这八个网是顶点传递的，而不是面对面传递的，分别是cem，fes，fsz，fxt，hca，htb，kgm和tts（请参阅表S2，ESI †）。它们通常被称为阿基米德网络，而所有顶点传递网络一起称为开普勒网络或开普勒-舒布尼科夫网络。21从图1d中可以看出，kagome网（kgm）由三角形和六边形组成。在每个顶点处，两个六边形和两个三角形相交。由于六边形和三角形以交替的方式围绕顶点，因此该顶点的Schläfli符号为3.6.3.6。具有正多边形的网的第三重要组是20个网，它们恰好包含两种类型的顶点-所谓的非规则网（请参见表S3，ESI †）。一个例子是krb网，它由两种类型的面组成：六边形和三角形。在一个顶点（在图1e中用实心圆表示）中，六个三角形相交。因此，Schläfli符号为3 6。在另一个顶点（实心圆，Schläfli符号3 4 .6），一个六角形和四个三角形相交。包含不规则多边形的网大多包含不规则五边形，例如所谓的Cairo平铺mcm。该网络也可以用作引入对偶概念的示例：通过在其中心点用新顶点替换面来形成对偶网络。图2a中显示的开罗拼贴就是这种网络的一个示例，因为它是tts的对偶净。根据O’Keeffe及其同事介绍的术语，因此20也可以称为tts-d，其中-d表示对偶关系。除了这些基本的平铺之外，sql网络的上层结构Lieb格子最近引起了很多关注。22,23与sql net 相比，它在正方形边缘的中间有一个额外的中心（请参见图1f）。在表S1-S4（ESI †），可以找到总共101种拓扑的草图，所有这些拓扑都包含在RCSR数据库中。他们是伴随着他们的TB带结构，既为根本网（只有1 日 -Neighbour相互作用），并与其中两个1化学更现实的TB模型ST -和2 次 -Neighbour互动都考虑在内。另外，考虑了自旋轨道耦合。对于某些包含不规则多边形的网络，顶点的排列对应于hxl网络。但是，某些顶点并未与其所有邻居相连，这导致这些网络中出现不规则多边形（见图2b）。对于两个代表性的例子）。由于这种复杂性，它们被认为不太可能在2D聚合物中实现。因此，这项工作仅包括具有规则多边形的平铺图和很少选择的具有不规则多边形的网状图。
图1 显示了常规hcb（a），hxl（b）和sql网（c），半规则kgm网（d），非规则krb网（e）和Lieb晶格（ F）。在网络草图（第1列）中，不等价的顶点由实心和空心圆表示，而krb中的蓝色边缘表示这些连接与黑色的不等价。红色虚线表示单位单元。（第2-5列）计算的带结构仅考虑（从左到右）第一次邻域相互作用，即1ST -和2 次 -Neighbour相互作用，1 日 -和2 次 -Neighbour与自旋轨道耦合（SOC），以及用于1D带的能带结构的相互作用。能量是在1单位给出ST -Neighbour跳频| β 1 | （请参阅第3节）。（g和h）具有六边形和正方形对称的网的具有高对称点的第一个布里渊区。
图2 （a）通过将顶点放在面的中心并删除旧顶点，可以获得给定拓扑的双网。所述MCM净是双重的TTS净（和，因此，也被称为TTS-d ），因为它可以通过将顶点在所述正方形和三角形的中心而获得的TTS净。反之亦然，tts网是mcm网的对偶，可以通过将顶点放置在mcm的不规则五边形的中心来获得。由于mcm由不规则多边形组成，这是不规则网的一个例子。（b）两个不规则网的例子，它们的几何结构与其他网相同，但链环缺失。这样的例子不包括在本调查中。
3 网络施加的电子结构
3.1 网络连接性对电子结构的影响
在本节中，我们将演示网络连接性如何确定电子结构的重要功能。为了演示，我们讨论了两个相关的柏拉图网，即hxl和hcb网，如图1所示。我们进一步假设每个顶点一个电子，也就是说，能带结构中正好占据了一半的电子态。
的HXL晶格具有三角形结构，其中具有六个邻居的每个顶点的坐标。hxl中的所有顶点都是等效的，因此相应的能带结构仅包含一个带，该带必须被半填充，因此迫使hxl网络成为金属。该HCB网，而另一方面，由正六边形，其中每个顶点有三个邻居相连的。它在晶胞中有两个位点（相同，但具有不同的环境），从而产生两个带，它们仅在高对称K点处相交，形成了所谓的狄拉克点。由于带已充满一半，所以费米能级（E F）恰好位于狄拉克（Dirac）点，在非相对论极限内，无质量费米子出现。它们导致极高的电荷载流子传输。
从hxl和hcb网络之间的差异，我们看到网络的连通性是形成电子结构的决定性因素。将网络连接性转换为Schrödinger方程模型的最简单形式是TB模型。我们假设一个共轭π电子系统由每个顶点一个有效的p z轨道形成。原子轨道（LCAO）拟设的线性组合与这些P只由ž轨道（相当于休克尔理论的芳族分子24），和第一我们只考虑1 ST -Neighbour相互作用（参见图3）。
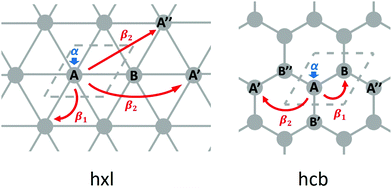
图3 图示的TB参数：现场能量α，1 日 -Neighbour跃迁积分β 1，和2 次 -Neighbour跃迁积分β 2，对于HXL和HCB网。单位单元用虚线表示。
相当于理论休克尔，最简单的TB近似内，每个顶点有助于一个现场能量α（典型地设置为零），且每个1个ST -Neighbour相互作用跳频贡献β 1（典型地设置为-1，以便使能量在单位的| β 1 |，参见图3。 ）。
对于HXL网，其中仅具有每单元电池一个顶点，哈密顿由表达式给出 与波矢ķ\，和δ\ 1是连接顶点到其1个矢量ST邻居。在hcb中，这是顶点A及其相邻节点B，B’和B’’之间的连接（图3）。对于具有n个顶点的网络，它将变为n × n矩阵： 周期性hcb系统的哈密顿量可以使用Bloch理论轻松求解，25，相应的能带结构如图4所示。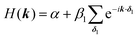
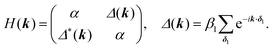。E F被定义为布里渊区（BZ）中的最高占用状态。确定半导体的E F是很容易的（每个带包含2个电子）。对于金属，需要进行数值积分，其中在BZ中放置了N G个点的数字网格，每个网格点每个带贡献2 / N G个电子。栅格点从最低能量到较高能量（aufbau原理）被占据，直到满足每个单位单元的电子数量为止。
图4 的带结构HCB净考虑（a）仅1 ST -Neighbour相互作用（左）以及还有2 次 -Neighbour相互作用（右）; （b）加入SOC，以λ = -5.8×10 -6 β 1，24为石墨烯（左）的值，和λ = 0.1 β 1（右）。左图中的插图放大了K点处的能带结构，并显示了Dirac点处的微小间隙开口。（c）六溴环十二烷的能带结构宽度为12个单位的纳米带，以及六溴环十二烷网的Wannier电荷中心（WCC）演变。这里，我们使用一种夸张的值的λ = 0.1 β 1，使供示范的效果显著。
TB模型的第一个扩展是包括第二邻居（可能更高）的交互。对于hxl晶格，到第二个邻居的几何距离和拓扑距离不同（第二个邻居都是距离2个链接的顶点）：图3中的A’和A’’都是A的第二个邻居，但是它们具有不同的几何距离。这里，我们把所有拓扑2 个平等邻居，和任意选择的值β 2 = 0.1 β 1，这是相当大的，因此稍微放大2的影响第二波段结构上的邻居互动。通过设置很容易说明是否包含第二邻居互动。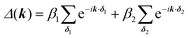
对于hxl和hcb网络，第二邻域的相互作用仅会稍微改变条带的形状（请参见图1和4a），但它们对其他网络的影响更大（请参见第4节）。
3.2 电子拓扑和自旋轨道耦合
石墨烯的许多令人兴奋的特性之一是它是原型2D拓扑绝缘体（TI）的事实。拓扑特性是自旋-轨道耦合（SOC）的直接结果，我们将其包含在TB哈密顿量中，其方式与Kane和Mele的开创性工作中概述的方式相同。26固有SOC项取决于第二邻居的相互作用。哈密顿并且因此波函数变得自旋极化，并且写为：β\SOC= -iνIJλ小号\Ž，其中ν IJ = δ 1 × δ 2 = 1 ∨
-1表示电子从顶点i到达j时路径的方向。例如，在图3中，当电子从A通过B’’到达A’时，它进行逆时针旋转，因此ν = 1，相反，从A到A’’的SOC为ν = -1，顺时针旋转。λ和S\ z分别表示SOC常数和保利矩阵。值得注意的是，通过添加SOC并考虑自旋，哈密顿量从2×2矩阵扩展到4×4矩阵。自旋非偏振参数α，β 1和β 2因此需要乘以2×2单位矩阵I\ 2。
图4a和b比较了有和没有SOC 的hcb能带结构。作为一个重量轻的元件，碳的SOC是微小的（λ = -5.8×10 -6 β 1 26），并且因此产生0.02兆电子伏的一小带隙（见插图的4B图）。SOC增加至0.1不切实际的夸张的值β 1清楚地示出的带隙和开口是用于获得2D聚合物的拓扑性质有用（参见图4c）。
重要的是要注意，尽管SOC引起的带隙打开是拓扑状态的必要条件，但它不是一个足够的条件（即，打开的带隙可能在拓扑琐碎的状态之间）。观察拓扑状态是否位于E F上的最简单的方法（虽然既不优雅也不计算经济）是计算纳米带，该纳米带明确产生拓扑边缘状态。图4c的左侧显示了一个宽度为12个单位的锯齿形hcb纳米带的能带结构。考虑到SOC产量的计算，除了由于对称性降低而导致的更复杂的能带结构之外，开放带隙和穿过E的状态都在Dirac点所在的位置处为 F。
值得注意的是，材料的拓扑特性是其体积（材料内部）的结果，并且拓扑边缘状态仅在其边界处显示。因此，无需进行显式的纳米带计算即可证明拓扑状态。这些计算需要利用空间拓扑结构和Berry相的概念。27在数学中，拓扑是一种几何属性，将在变形下保留。例如，在三个维度上，具有闭合表面的球体的类（g）为零。属将在变形下保存：保持封闭曲面的任何几何变换（例如，从球体到任何多面体）都将保持g=0。具有孔的圆环（甜甜圈形）的特征在于g =1。在拓扑上，甜甜圈可以转换为带有孔的任何其他对象，例如转换为杯子。但是，圆环和球体不能相互转换。
在二维中，可以使用高斯-邦尼定理来计算区域的拓扑： 其中a表示区域，K是高斯曲率。的磁通类似物ķ在带理论是浆果曲率˚F 米 =∇ ķ\ × 阿*米，其中**阿*米，贝里连接或浆果电位被定义为*阿*米 = 我 < ù 中号 |∇ *ķ** | u m〉。它指示在Bloch状态u的规范变换下的电磁矢量电势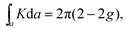
米*。
与高斯曲率定理中高斯曲率的积分相似，当Berry曲率在BZ内积分时，它成为Berry相，并进一步除以2π，我们得到的Chern数定义为： 对于频带m。Chern数是整数，如果不为零，则表示拓扑上不重要的带。此外，在整数量子霍尔效应（IQH）中，霍尔电导率 与所有占据能带的Chern数之和C tot成正比。HCB结构的最低带和最高带的Chern数分别为1和-1，这再次证实了这些带在拓扑上确实是不平凡的。
Zhang 等人发现的量子自旋霍尔效应（QSH）。图28最佳地示出了拓扑绝缘体中的拓扑保护边缘状态。但是，自旋相关的拓扑特性不再可用Chern不变量来表征，因为在时间反转对称性下，总的Chern数将由自旋向上和自旋向下的电子抵消。这个新的不变量称为Z 2，其计算公式如下： 超过BZ的一半的积分遵循 沿K点路径的时间反转对称性。该ž 2
不变量只能是0（在拓扑上是平凡的）或1（在拓扑上是平凡的），并且是针对整个电子系统给出的，与Chern数相反，不是每个频带。
提出了多种计算Z 2不变性的方法，例如通过波函数29的奇偶性和Fukui-Hatsugai方法。30在这里，我们采用Soluyanov和Vanderbilt（31，32）给出的方法，该方法适用于Wannier充电中心（WCC）。根据定义，对带中的化函数米的位置处- [R\可以写为 其中V是晶胞体积，d是系统的维数，并再次ü是布洛赫波函数。WCC是第一个单位单元中Wannier函数的平均电荷位置。沿轴定义为
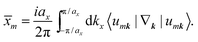使用这些WCC，可以通过在BZ的一半上画线来获得Z 2不变性。对于拓扑上不重要的系统，任何穿过一半BZ的线都应越过WCC奇数次（有关过程的更多详细信息，请参见Z2PACK封装33的说明）。在图4c中，在BZ的一半处任何相交的线都与WCC相交一次，这表明hcb结构是Z 2 = 1 的拓扑非平凡材料。
3.3 网络确定的电子能带结构和拓扑特性
现在，我们讨论网络对遵循网络对称性的材料的电子特性的影响。我们注意到，在2D聚合物中，顶点由分子构建单元表示（并且一个分子可以提供多个顶点）。两个顶点和π离域的程度之间的距离限定了1 ST -Neighbour TB跳频元素β 1非零2，和被排列的较长的离域的结果ND -Neighbour TB跳频元素β 2。系统中电子的数目由代表顶点的分子给出，并可以通过功能化控制（例如，将碳原子替换为B（N）会降低（增加）每单位电子数）。12
由于规则网络hxl和sql仅由一个顶点构成（请参见图1b和c），因此它们的能带结构仅包含一个能带。它与抛物线的顶点出现在Γ点处。如果填充一半，则系统必须是金属的。2 个 -Neighbour相互作用稍有改变波段的色散，并且缺乏顶点之间的相互作用（β 1 →0）产生自旋中心的网格。如果该带为空并标记了导带（CB），则其色散将确定Γ点处载流子的有效质量。如果该带是完全填充的价带（VB），则M处将出现空穴 点。
如果晶胞中存在第二个顶点，则也存在两个波段。这是的情况下HCB晶格，其从出现HXL晶格，当每3 次顶点被移除以形成蜂窝结构。因此，在K点，抛物线消失，所有带在圆锥形相交处交叉，称为Dirac点。该点还在能级上将所有频带分成两半，从而将E F固定到Dirac点。在2 次-邻域相互作用改变了能带色散，但不影响狄拉克点处的高度对称锥形能带结构，这使得简单的TB方法足以描述石墨烯中的物理现象。
因此，每晶胞的第三个顶点会生成第三个波段。这些结构之一是kgm晶格，可以从hxl晶格中再次删除第四个顶点来获得它。从hcb晶格可知，其能带结构（参见图5）包括狄拉克点，以及在能量最高的Γ点处接触狄拉克带的平坦带。的2 次 -Neighbour相互作用只对能带结构小的影响。如果能带结构是半填充的（单位晶胞中有三个电子），则kgm晶格是金属的。但是，如果每个晶胞仅存在两个电子，则它具有与hcb相同的特征，如果电子超过三个，则可以访问平坦带。在这一点上有趣的是，可以通过官能化来控制平坦带的分散。12
图5 仅考虑第一个邻居（左上），第二个邻居（右上），SOC（左下）和第二个邻居（具有SOC（右下）） 的kgm晶格的能带结构。显示了各个频段 的陈恩数C。
另一个有趣的具有三个条带的结构是Lieb晶格，该sql晶格删除了第 4 个顶点，从而产生了三个位点（其中只有一个严格地像是与sql晶格一样是具有4个链接的顶点，其他两个只有2个链接）（图1和6）。图6所示的结果带结构显示了一个狄拉克点，该点与一条平坦带交叉。每个晶胞具有三个电子，E F位于狄拉克点。的2 个 -Neighbour相互作用打开平坦，未占用频带之间的带隙小。
图6 利勃晶格的能 带结构。约定如图5所示。需要注意的是夹杂物的2 个 -Neighbour相互作用通过的距离判据产生不同的值β 2，这将分散平带。
SOC的引入主要影响高对称点。对于sql和hxl，在TB模型中，SOC效果完全抵消。对于在第3.2节中讨论过的hcb晶格，SOC表现出其拓扑性质，既用Chern数又表示为Z 2不变式。在费米能级的交叉带中很容易看到它们，它们标志着受拓扑保护的线性带，可提供无耗散的自旋传输。
对于kgm晶格，SOC都在Dirac点处打开了带隙，并在Γ点处打开了平坦带和Dirac带之间的接触点。这三个带在拓扑上都是不平凡的，如Chern数和Z 2不变式所反映（见图5）。
在Lieb晶格中，SOC在Dirac点处打开带隙，但不移动平坦带。因此，它创建了一个有趣的电子结构，在平带中具有重电子，在狄拉克锥的前沿带中具有无质量的电荷载流子。虽然形成狄拉克锥的带在拓扑上是不平凡的，但利勃晶格中的平坦带仅显示出微不足道的拓扑特性（请参见图6）。
3.4 2D网络的电子结构
表S1-S4在ESI †显示草图和对应的TB电子结构，包括1 日 -和2 次以下101个网-Neighbour相互作用以及自旋-轨道耦合，：表S1（ESI †）示出了这些用于柏拉图网hcb，hxl和sql。表S2（ESI †）包含阿基米德网络cem，fes，fsz，fxt，hca，htb，kgm和tts的这些图。非规则网状的蜂鸣声，CPH，KRA，KRB，KRC，KRD，KRE，KrF受，KRG，KRH，KRJ，KRK，KRL，KRM，KRN，KRQ，KRR，KRS，KRT，和USM列于表S3（ESI列出†）。表S4（ESI †）包含bex，bey，bhd，car，cem-d，cpa，cpb，cpc，cpd，cpe，cpf，cpg，cpj，cpk，cpl，cpm，cpn，cpo，cpp，cpq，cpr，cps，cpt，cpu，cpv，cpw，cpx，cpy，cpz，cqa，cqb，cqc，cqd，CQG，CQP，CQR，CRU，CRZ，DHA，DHB，ESQ，FWB，FWE，HCA-一个，HNA，HNB，HTB-一个，JVH，KGD，KGD-A ，克鲁，KRV，韩元，KRX，KRY，MCM，MTF，PNB，PND，PNE，PNF，png，pnh，sdb，sdc，sdd，sde，sdf，stz和suz网络。
4 培育拓扑特性
如第3节所示，二维材料的能带结构的重要特征从网络拓扑中浮现出来。特别是，拓扑属性与网络的连通性直接相关。我们已经发现了大量具有吸引人的电子，潜在拓扑性质的网络。由于2D聚合物仅由轻元素制成，因此SOC的大小很小，并且出现的带隙仅在约20μeV的范围内。因此，只能在极低温条件下探测这些特性，因此限制了它们的应用。最近，伯卡德（Burkard）研究小组表明，如果该材料在幻角下与过渡金属二卤化钨界面接触，则可以显着增加石墨烯中的SO诱导带隙。34 对于2D聚合物，这样的效果也是可能的。
一种增加带隙的化学方法是量子限制的明智应用：石墨烯纳米带由于其有限的宽度而打开了带隙，如果带的形状适当，它们将保持其拓扑性质，从而产生具有大带隙的拓扑绝缘体。35–37
在这里，我们将探索一种不同的化学方法来创建2D拓扑绝缘体：我们的目标是通过减少2D网络的对称性来在拓扑上不重要的点上打开带隙。本节的其余部分将说明这种方法。
对于柏拉图晶格sql，hxl和hcb以及阿基米德净重kgm，所有顶点和边缘在化学上都是相等的，并且晶格对称性降低不是控制电子和拓扑特性的简单方法。
该利布晶格具有两个不同的位点：一类是连接到四个相邻顶点，而第二类是位于连接到两个相邻的边缘的部位。链接都是相同的。由于两个对称的不同位点将由两个不同的分子结构单元表示（请参阅第5节），因此它们可能具有不同的化学势，在TB方法中，化学势用两个不同的α值表示。实际上，α的这种变化在狄拉克点上打开了一个带隙。为简单起见，我们展示了与乐队只考虑1个的效果ST -Neighbour相互作用。有趣的是，如果四个连接的顶点的化学势低于线性位点的化学势（参见图7）），则间隙开口位于平坦带的下方，而如果线性位点的化学势较低，则间隙开口位于上方。请注意，在两种情况下，狄拉克带之一都接触平坦带。由于不同的化学势导致的能带开放增强了3.3节中讨论的SOC诱导的能带开放，而三个能带的拓扑特征保持不变。因此，减少对称性可以增加拓扑点之间的间隙，并为实现室温二维拓扑材料提供了一种有希望的方法。
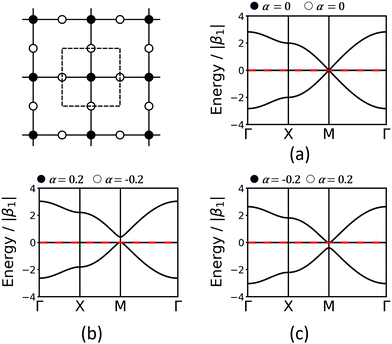[](https://pubs.rsc.org/image/article/2020/cs/c9cs00893d/c9cs00893d-f7_hi-res.gif)**图7层** 利布只考虑1带结构ST -Neighbour相互作用和不同现场能量，α。
的FES晶格（图8）具有相同的顶点，但不同的对称性中的边缘，这要么是八角形之间（红色图8）或正方形和八边形（在黑色之间图8）。在具有相同的跳频元件TB模型β 1，它示出了两个高对称交叉点（Γ和中号），两者都具有三个条带，其中之一是局部平坦，而在一狄拉克点的其他两个交叉。这些简并性在SOC的作用下被打破，并且所有四个带在拓扑上都不是平凡的（见图8a）。）。由于不同分子连接物将代表在2D聚合物的不同边缘，系统必须具有不同的值来描述β 1。如图8所示，与Lieb晶格类似，这种对称性降低在相同的高对称点处打开了带隙。根据SOC的值，所得的频段可以更改其Chern数。
图8层。 指环结构FES：（a）考虑1 日和2 个邻居和SOC，（B-d）只考虑1 ST -Neighbour与跳频矩阵元素的相同的和不同的值相互作用β 1和β 1 ‘。
最后，我们研究作为非规则网络成员的krb晶格（参见图9）。晶胞包含八个位点，其中两个具有六个邻居（黑色标签），六个具有四个邻居（白色标签），它们产生八个波段。两个不同的边缘分别被涂成黑色和蓝色。能带结构在M，K和Γ处显示出一些简并的晶格点。所有四个较低的带在拓扑上都是微不足道的。然而，具有两个不同的顶点和两个不同的边缘允许一个宽范围的电子结构变形例的，因为这两个α和β 1可具有不同的值。与利勃类似修改现场元素将在Γ点打开带隙。跳跃元素会影响频段的总体色散。我们得出结论，存在适用于化学势变的化学敏感概念并调整π共轭的合理设计规则，这些规则可用于设计具有特定应用电子特性的拓扑和经典2D聚合物。
图9层 的带结构KRB只考虑1 ST -Neighbour相互作用（a）中，跳频元件（b和c）和现场元件（d和e）的变形例。约定如图7和8所示。
5 在2D聚合物结构中实现2D网络
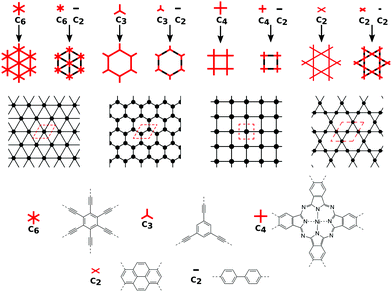
为了形成具有正确拓扑的2D聚合物，必须组装分子构件。如若干评论所示，可以通过分析所需网络的拓扑图来获得所需的顶点和边缘的形状和对称性。2,38–41这种拓扑图可以在图10中找到。虽然边缘通常是线性的，并且不施加任何其他要求，但顶点需要具有正确的旋转对称性。在RCSR数据库中的200个不同的二维网包括具有配位数顶点从3至12 20中最丰富的是被3,4，和6的邻居顶点。因此，单体需要具有C 3，C 4（或具有四个连接点，但对称性破坏了，C 2）和C 6旋转轴分别用作这些顶点。另外，C 2单体可以放置在边缘上。为了给出这些情况的示例，图10显示了如何将hxl，hcb，sql和kgm网络与单体示例一起解构为顶点和边缘。
图10分别显示了 带有和不带有明显链接程序的hxl，hcb，sql和kgm网络的 拓扑图以及相应的2D表示（单位单元标记为红色）。图的底部显示了具有2倍，3倍，4倍和6倍旋转对称性和线性接头的简单节点的建议。
这些网既可以通过具有各自旋转对称性的顶点的自缩合，也可以通过这种单体与连接体的连接而获得。早在1980年代，有人就提出了γ-石墨烯作为hxl网络的一个例子。42在这种材料中，苯顶点通过乙炔基相连。对于具有hcb拓扑的共轭聚合物，三角形的顶点（C 3旋转对称性）通常是苯环，稠合苯环，或者到目前为止（仅在计算研究中考虑）还是简单的叔丁基。9,13,43–45对于sql net，通常为C 4选择的构建基块是卟啉或酞菁，它们的晶格角为90°。14,46但是，使用pyr或四亚乙基作为带有四个连接器的结构单元（旋转对称性降低为C 2）会导致大量扭曲的sql结构。10,13,14,47此处，尽管像元向量之间的角度不同于90°，但由于顶点的连通性和同一性，二维聚合物仍处于sql拓扑中。类似地，四亚乙基顶点也可用于实现2D聚合物中的kgm网。47使用共轭五元环可导致形成具有异常htb拓扑的2D聚合物。48除了非常流行的网以外，最近还合成了相当复杂的网，例如bex网。49与对应于一个电子结构的2D聚合物利布晶格参展斯通铁磁性报道通过姜等。（参见图11）。15
图11 的示意性表示利布晶格（a）和相应的TB带结构（b）中。（c）中顶部和PY（BCSB）的晶体结构的侧视图2与PY（蓝色椭圆形）和BCSB（红色椭圆）配体坐在扭曲的角落和边缘中心部位利布分别晶格。（d）DFT计算出k z = 0平面的电子能带结构，以及p z（黑圈）和p x，y（绿圈）轨道的轨道分辨投影带。红色和蓝色乐队突出了Lieb-3和Lieb-5带结构。与（b）相当的Lieb签名在导带中用红色虚线矩形标记。（c和d）经ref许可改编。13，版权所有2019，Springer Nature。
作为连接基，已经使用了乙炔基结构单元（到目前为止，大多数情况下是在计算研究中）和通过亚胺键连接至顶点的苯环。9,10,13,14,45,47它们都很简单，可以保证共轭，并且相当坚固。但是，如果苯单元相对于平面顶点具有二面角，则可以减少轨道重叠。因此，重要的是设计链接器，使其尽可能保持平面。但是，在由稠合苯环组成的接头中，连通性迫使系统呈平面状。在这种情况下，π轨道重叠被最大化。44,46如果分子结构单元中代表顶点和边缘的前沿轨道的能量匹配，则可以改善分散带的形成。15单体之间电子耦合的强度可以通过查看二聚体模型中的电子离域来估算。14控制二维聚合物能带结构的一个很好的例子是组合的 kgm-hcb网，如图 12所示。12晶格是由杂三烯构成的，其中中心原子可以是B，C或N，因此会形成一个无人居住，半人居住或完全有人占的中心位置。因此， ê ˚F位于狄拉克带（B）的下方，在狄拉克点（C）或狄拉克频带上述（N）（图12A-C）。带的分散（在平坦带中最明显）受单体化合物中的桥基强烈影响，可以选择CO，CH 2或O。在具有B个中心原子的单体的情况下，平坦带标记价带最大值。孔的有效质量范围为1.6 m e至无穷大（见图12d–f）。
图12 ：kgm晶格（a）的示意图，以及基于杂三烯酮的二维聚合物的原子结构（b）和相应的能带结构（c），揭示了kgm的特征（参见图5）。根据电子数，E F移至狄拉克能带（B）以下，狄拉克点（C）或狄拉克能带的顶部（N）。通过B和N的官能化，可以访问从kgm晶格出现的平坦带。具有三个不同桥基的杂三烯，即（d）酮，（e）CH 2和（f）醚对平带的色散表现出不同的影响。能带结构是kgm和hcb网络的叠加，两者均在此2D聚合物的结构中找到。改编自ref。10，美国化学会2019年版权所有。
如果拓扑带在E F附近，则只能获得拓扑相。除了先前的先决条件外，对于某些系统，可能有必要将E F转移到拓扑上很重要的位置。这可以通过功能化12（图12a和c），并在某种程度上通过掺杂来实现。
其他人在本期特刊或Liu 等人的论文中详细讨论了保留π共轭的合适偶联反应。50
6 展望与观点
拓扑绝缘子的发现标志着凝聚态物理的突破，但是在室温应用中实现这种态的方法仍未解决。众所周知，晶格可以施加拓扑特征，正如已经针对光子晶体证明的那样，例如在光学利勃（Lieb）晶格中。51–54尽管这种方法可以研究晶格施加的拓扑效应，但对玻色子粒子的限制限制了其应用。因此，在材料中实现拓扑网络很有意思。
近来，通过由一氧化碳分子23的阵列限制的Cu（111）的表面状态电子或Cu（100）表面上的氯超结构的空位缺陷形成Cu（111）的表面状态电子，通过实验实现了Lieb晶格的边缘和顶点。22但是，这些结构仅在低温（<5 K）下稳定。
另一方面，相对较新的骨架材料领域，包括金属-有机骨架和共价-有机骨架以及2D聚合物，可实现几乎任何在室温下稳定的网络结构。这提供了将化学功能引入网络的另一种方式，即通过网络的结构拓扑。在这篇评论中，我们通过专注于实现拓扑2D网络的材料来探讨了可能性的表面。
网状化学结构资源数据库中包含的200多个网络的集合20为实际的2D材料提供了多种可能的骨架，可以通过适当选择分子构件来创建骨架。然后，可以在此类构件的相应2D布置中实现假设2D网络的拓扑特性。正如我们在本教程中所展示的那样，使用具有长距离π共轭作用的结构单元创建2D聚合物是实现具有高结晶度和扩展π共轭关系的拓扑网络的非常有希望的途径。在这里，我们展示了如何预测网络的拓扑特性，如何生成材料的原子结构，并展示了在实验中成功实现的示例。本期特刊的其他作者在一篇文章中介绍了合成这些材料的关键步骤。
尚待解决的重大挑战之一是设计包括活性位点的结构单元，该活性位点通常意味着不饱和π电子。也就是说，结构单元必须是π自由基，仍然可以进行预先设计的连锁反应。备选地，在聚合之后，可以例如通过合成后官能化或通过门控来控制π电子的数量。
第二大挑战是控制缺陷的水平，包括结构缺陷和替代缺陷。第三个相关的重大挑战是高结晶网络的形成，因为高结晶度是拓扑特性鲁棒性的前提。这包括框架的刚度，因为强大的晶格振动可能足以使拓扑特性崩溃。
鉴于2D聚合物化学领域的巨大进步以及凝聚态物质物理学家与化学家之间跨学科合作的最新发展（例如，在石墨烯纳米带的研究中显示） [35,36]，我们有信心在未来十年内能够应对这些挑战。
在这篇综述中我们没有触及的是由层间相互作用产生的附加功能：在多层和异质结构中，预计这些2D材料的特性会进一步修改，这对于其他2D材料（包括石墨烯或过渡材料）是已知的金属二卤化物。我们在最近的一篇观点文章中介绍了该主题，并向有兴趣的读者推荐该文章。55